Cirkelns area, omkrets och cirkelbågar

För att beräkna arean och omkretsen av en cirkel används ett tal som heter Pi $(π ≈ 3,14)$. Med Pi ges arean av cirkeln genom följande formel $Area = π ⋅ r^2$. Omkretsen i sin tur ges av formeln $Omkrets = π ⋅ d$.

I detta inlägget kommer du lära dig allt om hur man beräknar arean och omkretsen av en cirkel. Det är en vanlig uppgift inom geometrin i matematiken och kan vara lite klurigt om man stöter på det för första gången.

Cirkelns radie och diameter

En cirkel definieras som en rund geometrisk form med en mittpunkt som ligger på ett konstant avstånd från kanten hela vägen runt cirkeln. Det konstanta avståndet mellan mittpunkten och kanten kallas för radie och brukar förkortas $r$.

Den runda kanten på cirkeln, eller cirkelns kurva, brukar kallas för cirkelns rand eller periferi och består av alla möjliga punkter på ett avstånd av en radie från mittpunkten.

Om man drar en rät linje över cirkelns mittpunkt från ena sidan till den andra får man vad som kallas för cirkelns diameter, som förkortas $d$. Diametern är alltså cirkelns bredd, eller avståndet tvärs över cirkeln. Fortsättningsvis har cirkelns diameter samma längd som två stycken radier efter varandra. Därför kan diametern beskrivas av formeln $d = 2⋅r$.

Talet Pi ($π$)

Det kan vara lätt att tro att man beräknar cirkelns area och omkrets på samma sätt som en kvadrat eller triangel, genom att endast använda sig av basen och höjden. Eftersom cirkeln är rund och saknar raka sidor är det dock svårt att mäta och beräkna med en linjal. Därför använder man talet Pi (som har symbolen $π$) för sådana beräkningar.

Talet Pi definieras enligt följande formel: $π = \frac{omkrets}{area} ≈ 3,14$.

Pi blir alltid detsamma oberoende av cirkelns omkrets eller area och består egentligen av en lång följd av decimaler, men brukar avrundas till 3,14 för enkelhetens skull.

Beräkna cirkelns omkrets och area

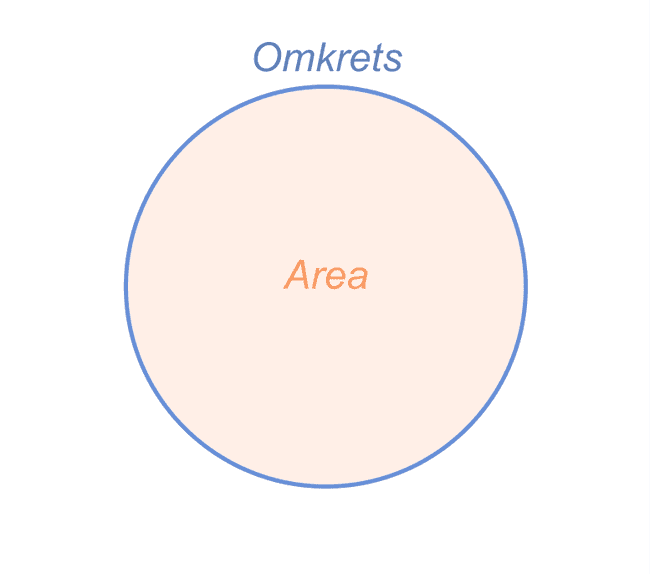
När vi nu definierat talet Pi ($π$) kan vi nu använda det för att beräkna cirkelns omkrets och area. Med hjälp av π beskrivs omkretsen och arean med följande formler:

$Omkrets = π⋅d = π⋅2r$

$Area = π⋅r^2$

Cirkelsektor och cirkelbåge

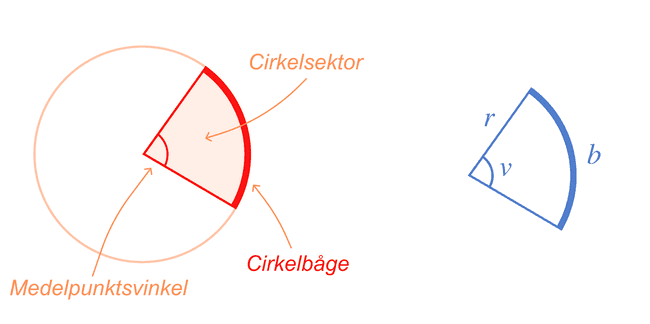
Utöver begreppen area, omkrets, radie och diameter finns det andra begrepp om cirkeln som kan vara nyttigt att känna till. Cirkelsektorn används är ett sådant begrepp, som kan förekomma i matteuppgifter inom ämnet geometri.

Cirkelsektorn kan beskrivas som en utskuren pizzabit eller pizzaslice, om hela cirkeln liknas vid en rund pizza. Kanten på pizzabiten eller cirkelsektorn kallas för cirkelbåge.

Den vinkel som bildas i spetsen av cirkelsektorn kallas ibland för medelpunktsvinkel. Vinkeln för en hel cirkel är 360°. Om cirkelsektorn är hälften av cirkeln kommer alltså medelpunktsvinkeln beräknas till $\frac{360°}{2} = 180°$.

Med hjälp av medelpunktsvinkeln $v$ kan man beräkna arean för cirkelsektorn, vilket även kan beskrivas som delen av hela cirkelns area. Med formeln $\frac{v}{360°} ⋅ (cirkelns\;area)$ får vi arean för cirkelsektorn.

Om medelpunktsvinkeln $v = 120°$ och hela cirkelns area är $90 \; cm^2$ blir uträkningen:

$\frac{120°}{360°} ⋅ 90 \; cm^2 = \frac{1}{3} ⋅ 90 = 30 \; cm^2$