Vad är Pythagoras sats?

Inom geometrin beräknar man ofta omkrets och area av olika geometriska former. Kvadrater, rektanglar, cirklar och trianglar är några av formerna. I den här artikeln ska vi beskriva hur man räknar ut omkretsen för en rätvinklig triangel med hjälp av en formel som heter Pythagoras sats.

Det finns många områden där Pythagoras sats används, som i byggteknik, arkitektur och fysik, men framför allt inom matematikens geometri och specifikt trigonometri.

Med Pythagoras sats kan man räkna ut längden av en okänd sida i en rätvinklig triangel, givet de övriga två sidorna. Den rätvinkliga triangels raka sidor heter katet och den långa, diagonala sidan heter hypotenusa.

Vad är en rätvinklig triangel?

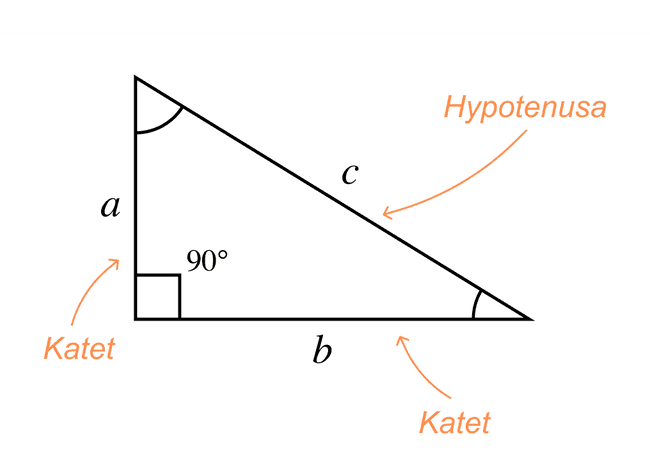
En rätvinklig triangel är en triangel där en av vinklarna är exakt 90°, alltså en rät vinkel. När man ritar vinklar i trianglar brukar de ritas som en båge eller halvcirkel, men en vinkel på 90° ritas istället som en fyrkant. Detta är för att man tydligare ska se att det är just en rätvinklig triangel.

I bilden nedan är även den rätvinkliga triangelns sidor namngivna. De har specifika namn inom matematiken. De två sidorna som möts i den räta vinkeln kallas kateter, och den långa diagonala sidan kallas för hypotenusa.

Hur fungerar Pythagoras sats?

Pythagoras sats beskriver förhållandet mellan längden hos en rätvinklig triangels alla tre sidor. Satsen beskriver att varje sida kan ses som en kant i en kvadrat, där arean av kvadraterna som bildas av triangelns raka sidor är lika med arean av kvadraten med hypotenusan som en kant. Det ges alltså av formeln:

$a^2 + b^2 = c^2$

där a och b är kateterna och c är hypotenusan i den rätvinkliga triangeln.

Man kan alltså säga att triangeln är rätvinklig om hypotenusan i kvadrat är lika med summan av kateterna i kvadrat, vilket kan skrivas som formeln:

$katet^2 + katet^2 = hypotenusa^2$

Visualisering av bevis för Pythagoras sats

Här har vi visualiserat de två kvadrater som utgörs av kateterna i den rätvinkliga triangeln. Summan av arean för dessa två kvadrater bildar sedan hypotenusans kvadrat.

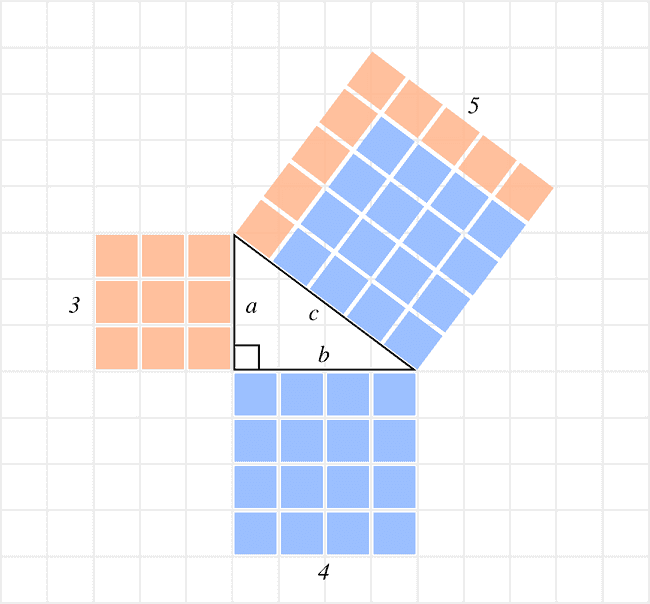
I detta exempel kateternas längder 3 respektive 4 rutor och hypotenusans längd är 5 rutor. Om vi använder oss av formeln vi lärde oss ovan kan vi räkna ut triangeln med Pythagoras enligt följande:

$3^2 + 4^2 = 5^2$

När vi räknar ut kvadraterna får vi följande ekvation:

$9 + 16 = 25$

Om man räknar de totala rutorna som kvadraterna omfattar ser vi att det blir samma som ekvationen ger oss.

Vad används Pythagoras sats till?

Ofta handlar räkneuppgifter där Pythagoras sats används om att ta reda på en okänd längd av en sida i den rätvinkliga triangeln. En sådan okänd längd brukar ibland beskrivas av en bokstav, så som bokstaven $x$.

Eftersom vi använder kvadrater i Pythagoras sats, alltså tal upphöjd till 2, kommer vi behöva använda roten ur för att få ut ett svar på längden. En sådan ekvation kallas för andragradsekvation.

Här följer ett räkneexempel:

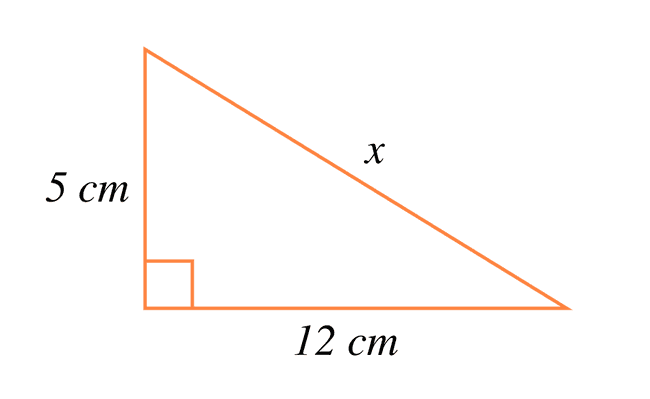
I denna uppgift måste vi ta reda på längden av hypotenusan i triangeln. Den okända längden är markerad med $x$. Triangelns kateter är $5 \; cm$ och $12 \; cm$. Om vi använder formeln vi lärt oss blir ekvationen:

$5^2 + 12^2 = x^2$

Vi börjar med att räkna ut $5^2 + 12^2 = 25 + 144 = 169$

Då vet vi att $x^2 = 169$ och kan då använda oss av roten ur för att få ut $x$.

$x = \sqrt{169} = 13$

Alltså är längden för hypotenusan $13 \; cm$