Allt du behöver veta om reella tal

Reella tal är tal som kan skrivas på en tallinje. Detta innefattar också alla de naturliga talen, heltal, rationella tal, samt alla tal som inte kan skrivas som ett bråk såsom pi. Reella tal är en av flera olika talmängder.

Vad är reella tal?

Ett reellt tal är ett tal som kan skrivas på tallinjen. Detta kan vara ett naturligt tal såsom 0 eller 1. Ett heltal såsom -10, eller ett rationellt tal såsom $\frac{1}{2}$. Ett tal såsom pi kan också vara ett reellt tal. Inom matematiken brukar de talmängden “reella tal” betecknas med bokstaven R.

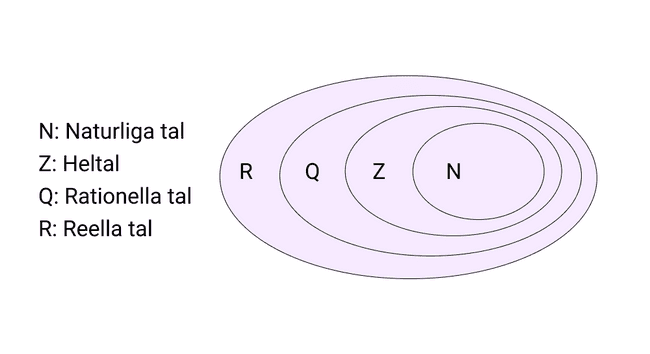
Bild ovan förklarar hur de olika talmängderna hänger samman. På bilden kan du se att rationella, heltal och naturliga tal delmängder av samlingsnamnet reella tal.

Under gymnasiet blir man introducerad till reella tal när man räknar på andragradsekvationer i matematiken. Detta beror på att det är först då som man stöter på komplexa tal, vilket är tal som inte kan skrivas på tallinjen.

Andragradsekvationer kan både ha komplexa och reella lösningar, och inom matematiken kan man exempelvis få ett problem där man ska ange alla reella lösningar. En reell lösning innebär att talet endast har en realdel, och ingen imaginär del.

Det bör även sägas att komplexa tal inte har något med att göra att det är svårt, utan det är endast en ny sorts tal som inte kan skrivas på tallinjen.

Skillnaden mellan reella och komplexa tal

Det finns tal som inte är reella och de kallas för komplexa tal. Ett komplext tal går inte att skriva på tallinjen och kan ses som en utvidgning av de reella talen. För komplexa tal lägger man till ytterligare än dimension på tallinjen, vilket gör att tallinjen både har en x- och y-axel.

Komplexa talet z skrivs som $z = a + ib$ där a är realdelen, och reella talet b är imaginärdelen och i är den imaginära enheten där $i^2 = -1$.

Under gymnaiset blir man introducerad till komplexa tal under avsnittet andragrads-ekvationer. Ett exempel på en ekvation som har en komplex lösning är ekvationen $x^2=−9$. Denna ekvationen saknar reella lösningar eftersom det inte finns något reellt tal som blir -9 när man tar kvadraten av det. Ekvationen kommer däremot ha två komplexa lösningar vilket är -3i och 3i.

Hur ser man om en ekvation kan ha en komplex lösning?

När man använder sig av PQ-formeln så kan man se att lösningen kan ha en komplex lösningar om talet som tar roten ur blir negativt i lösning. Då kommer talet ha en imaginärdel, och därför vara ett komplext tal. Detta beror på att det inte finns något tal som man kan ta kvadraten av och få en negativ lösning.